[특강] 기업리뷰 분석 2
탐색적 데이터 분석(EDA)과 추천모형 적합
Dr.Kevin 10/29/2018
지난 포스팅에서 우리는 관심 있는 회사에 대한 기업리뷰를 수집하는 방법에 대해 알아봤습니다. 이번 포스팅에서는 수집한 데이터를 이용하여 몇 가지 간단한 분석을 수행해보겠습니다. 먼저 데이터가 어떤 형태로 되어 있는지 확인하기 위해 탐색적 데이터 분석을 실행하는 것이 좋습니다.
탐색적 데이터 분석 (Explortory Data Analysis)
탐색적 데이터 분석 방법으로는 고정된 형태가 없습니다. 보통은 summary() 함수를 사용하여 기초 통계량을 확인하고, 히스토그램이나 상자수염그림을 그려 데이터의 분포를 확인하곤 합니다.
이번 예제에서는 추천여부와 성장예상, 그리고 별점 데이터를 중점으로 몇 가지 인사이트를 찾아보는 작업을 실시하겠습니다. 먼저 RDS 파일을 불러와서 전처리를 실시하겠습니다.
# 필요한 패키지를 불러옵니다.
library(tidyverse)
library(stringr)
library(stringi)
library(lubridate)
library(magrittr)
# 그래프 제목으로 자주 사용할 회사이름을 지정합니다.
compNm <- '삼성화재'
# RDS 파일을 읽습니다.
dt <- readRDS(file = '../data/Company_Review_Data_삼성화재해상보험.RDS')
20~100점으로 되어 있는 별점을 1~5점으로 환산하였고, 편의를 위해 성장예상과 추천여부 컬럼을 범주형으로 변환하였고, 연도별 현황 분석을 위해 등록연도 컬럼을 신규로 추가했습니다.
# 별점을 1~5점으로 환산합니다.
dt[, 8:13] <- sapply(X = dt[, 8:13], FUN = function(x) x / 20)
# 추천여부 컬럼을 '추천'과 '비추'로 변환합니다.
dt$추천여부 <- str_extract(string = dt$추천여부, pattern = '추천(?= )')
dt$추천여부[is.na(x = dt$추천여부) == TRUE] <- '비추'
# 성장예상과 추천여부 컬럼을 범주형으로 변환합니다.
dt$성장예상 <- factor(x = dt$성장예상)
dt$추천여부 <- factor(x = dt$추천여부)
# 등록일자를 날짜형 벡터로 변환합니다.
dt$등록일자 <- as.Date(x = dt$등록일자, format = '%Y/%m/%d')
# 등록연도 컬럼을 추가합니다.
dt$등록연도 <- year(dt$등록일자)
ggplot() 함수를 이용하여 다양한 그래프를 그릴 예정인데, 나만의 테마를 미리 설정해놓겠습니다.
# 나만의 ggplot 설정을 지정합니다.
mytheme <- theme(
panel.grid = element_blank(),
panel.background = element_rect(fill = 'white', color = 'white', size = 1.2),
plot.background = element_blank(),
plot.title = element_text(family = 'NanumGothic', face = 'bold', hjust = 0.5, size = 14),
axis.title = element_text(family = 'NanumGothic'),
axis.text.x = element_text(size = 10, face = 'bold'),
axis.text.y = element_text(family = 'NanumGothic'),
axis.ticks = element_blank(),
strip.text.x = element_text(size = 10, face = 'bold', family = 'NanumGothic'),
strip.text.y = element_text(size = 10, face = 'bold', angle = 270, family = 'NanumGothic'),
strip.background.y = element_rect(fill = 'gray80', color = 'white'),
legend.title = element_text(family = 'NanumGothic'),
legend.text = element_text(family = 'NanumGothic'),
legend.position = 'bottom')
재직상태별 성장예상 및 추천여부 확인
전직과 현직 등 재직상태별로 회사의 성장성을 예상하고 추천 또는 비추천 여부가 달라질 것으로 예상할 수 있습니다. 과연 그런지 그래프로 그려보고 카이제곱 검정을 통해 확인해보겠습니다.
# 추천/비추 여부 막대그래프를 그립니다.
drawBarPlot <- function(data, workGb, var) {
# 빈도테이블을 생성합니다.
tbl <- data[data$재직상태 == workGb, c('회사이름', var)] %>% table() %>% t()
# 막대그래프를 그립니다.
bp <- barplot(height = tbl,
ylim = c(0, max(tbl)*1.25),
names.arg = rownames(x = tbl),
beside = TRUE,
# legend = TRUE,
main = str_c(workGb, var, sep = ' ') )
# 빈도수를 추가합니다.
text(x = bp, y = tbl, labels = tbl, pos = 3)
}
# 그래픽 파라미터를 설정합니다.
par(mfrow = c(2, 2), family = 'NanumGothic', mar = c(5, 4, 4, 2))
# 막대그래프를 그립니다.
drawBarPlot(data = dt, workGb = '전직원', var = '추천여부')
drawBarPlot(data = dt, workGb = '전직원', var = '성장예상')
drawBarPlot(data = dt, workGb = '현직원', var = '추천여부')
drawBarPlot(data = dt, workGb = '현직원', var = '성장예상')
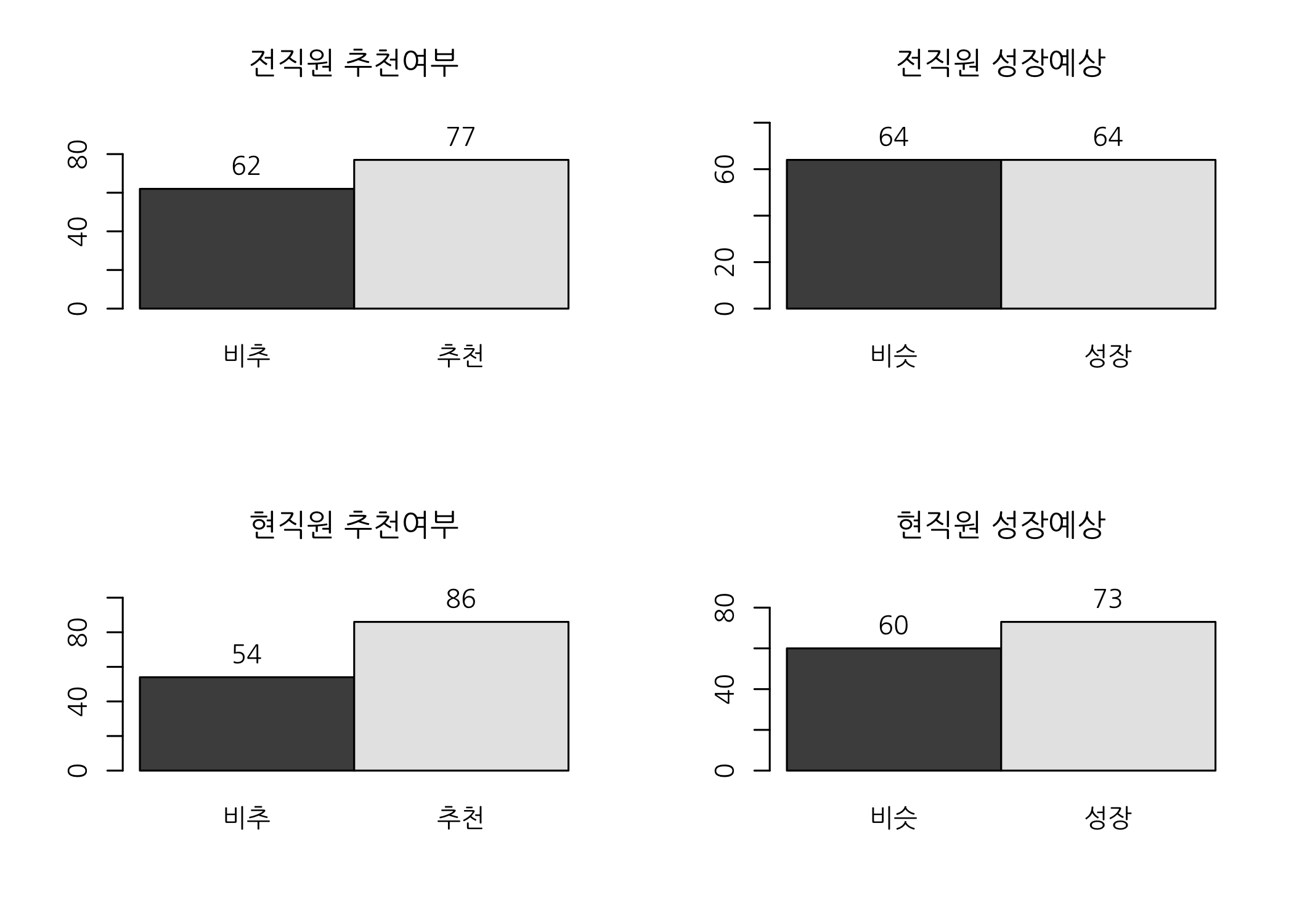
그래프 상으로는 재직상태별로 큰 차이가 보이지 않는 것 같습니다. 그럼 카이제곱 검정을 해볼까요?
# 필요한 패키지를 불러옵니다.
library(descr)
# 카이제곱 검정을 위한 사용자 정의 함수를 생성합니다.
chisqTest <- function(var1, var2) {
# 변수를 설정합니다.
v1 <- eval(expr = parse(text = str_c('dt', var1, sep = '$')))
v2 <- eval(expr = parse(text = str_c('dt', var2, sep = '$')))
# 빈도테이블을 생성합니다.
tbl <- table(v1, v2)
# 교차테이블을 생성합니다.
CrossTable(x = tbl,
expected = TRUE,
prop.r = FALSE,
prop.c = FALSE,
prop.t = FALSE,
prop.chisq = FALSE) %>%
print()
# 카이제곱 검정을 실시합니다.
chisq.test(x = tbl) %>% print()
}
# 재직상태 * 성장예상
chisqTest(var1 = '재직상태', var2 = '성장예상')
## Cell Contents
## |-------------------------|
## | N |
## | Expected N |
## |-------------------------|
##
## =============================
## v2
## v1 비슷 성장 Total
## -----------------------------
## 전직원 64 64 128
## 60.8 67.2
## -----------------------------
## 현직원 60 73 133
## 63.2 69.8
## -----------------------------
## Total 124 137 261
## =============================
##
## Pearson's Chi-squared test with Yates' continuity correction
##
## data: tbl
## X-squared = 0.44411, df = 1, p-value = 0.5051
# 재직상태 * 추천여부
chisqTest(var1 = '재직상태', var2 = '추천여부')
## Cell Contents
## |-------------------------|
## | N |
## | Expected N |
## |-------------------------|
##
## =============================
## v2
## v1 비추 추천 Total
## -----------------------------
## 전직원 62 77 139
## 57.8 81.2
## -----------------------------
## 현직원 54 86 140
## 58.2 81.8
## -----------------------------
## Total 116 163 279
## =============================
##
## Pearson's Chi-squared test with Yates' continuity correction
##
## data: tbl
## X-squared = 0.81148, df = 1, p-value = 0.3677
성장예상이나 추천여부 모두 유의확률(p-value)이 0.05보다 큽니다. 따라서 재직상태별로 차이가 없다는 귀무가설을 기각할 수 없습니다. 직관적으로는 전직원의 경우 현직원보다 해당 기업을 덜 추천할 것 같은데 이번 데이터로 분석해보니 반드시 그런 것만은 아닌 것 같습니다. 다들 좋게 좋게 헤어졌나 봅니다.
연도별 성장예상 및 추천여부 변화
# 연도별 현황을 확인합니다.
drawBarLinePlot <- function(data, workGb, var) {
# 등록연도가 없는 행을 삭제합니다.
data <- data[complete.cases(data$등록연도), ]
# 빈도테이블을 생성합니다.
tbl <- data %>%
dplyr::filter(재직상태 == workGb & !is.na(eval(expr = parse(text = var)))) %>%
select(c('등록연도', var)) %>%
group_by(등록연도, eval(expr = parse(text = var))) %>%
summarize(빈도 = n()) %>%
mutate(비중 = (빈도 / sum(빈도) * 100) %>% round(digits = 1L))
# 두 번째 컬럼명을 var로 변경합니다.
colnames(x = tbl)[2] <- var
# 홀수행의 비중을 NA로 치환합니다.
rowNums <- seq(from = 1, to = nrow(x = tbl), by = 2)
tbl$비중[rowNums] <- NA
# ggplot() 함수를 이용하여 막대그래프를 그립니다.
ggplot(data = tbl,
mapping = aes_string(x = '등록연도', y = '빈도', fill = var)) +
geom_bar(stat = 'identity', position = 'dodge') +
geom_text(mapping = aes(label = 빈도),
position = position_dodge(width = 0.9),
vjust = -1) +
geom_line(mapping = aes_string(x = '등록연도', y = '비중', color = var, group = var),
size = 1.2,
stat = 'identity',
position = position_dodge(width = 0.9)) +
geom_point(mapping = aes_string(x = '등록연도', y = '비중', color = var, group = var),
shape = 21,
fill = 'white',
stroke = 2.0,
size = 2.4,
stat = 'identity',
position = position_dodge(width = 0.9)) +
geom_text(mapping = aes(y = 비중, label = 비중),
fontface = 'bold',
position = position_dodge(width = 0.9),
vjust = -1.5,
hjust = 0.5) +
coord_cartesian(ylim = c(0, max(tbl$빈도, tbl$비중, na.rm = TRUE) * 1.1)) +
scale_fill_manual(values = c('gray80', 'gray50')) +
scale_color_manual(values = c('black', 'red')) +
ggtitle(label = str_c('연도별', workGb, var, sep = ' ')) +
mytheme +
theme(axis.title = element_blank())
}
# 연도별 현황을 그립니다.
drawBarLinePlot(data = dt, workGb = '전직원', var = '성장예상')
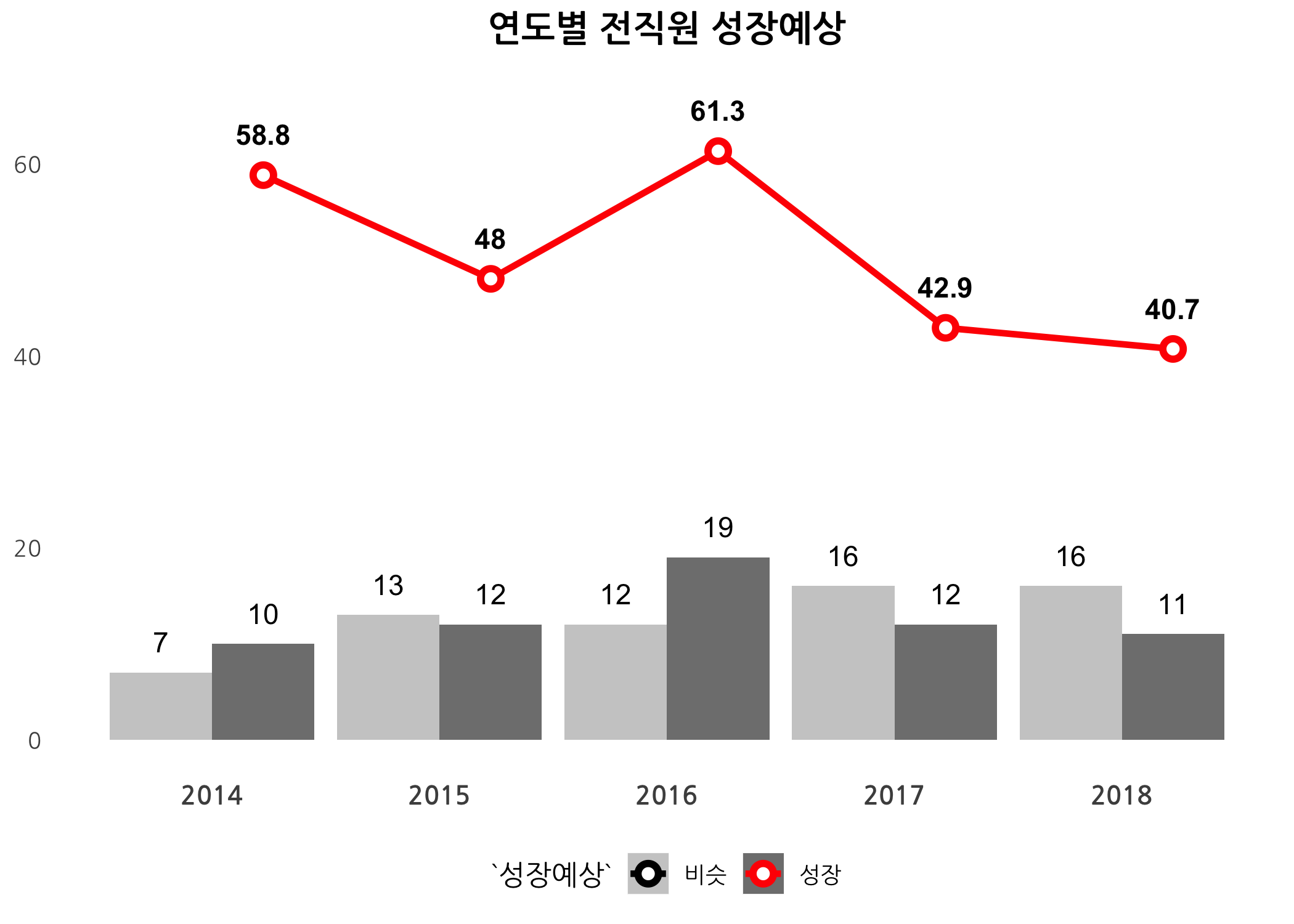
drawBarLinePlot(data = dt, workGb = '전직원', var = '추천여부')
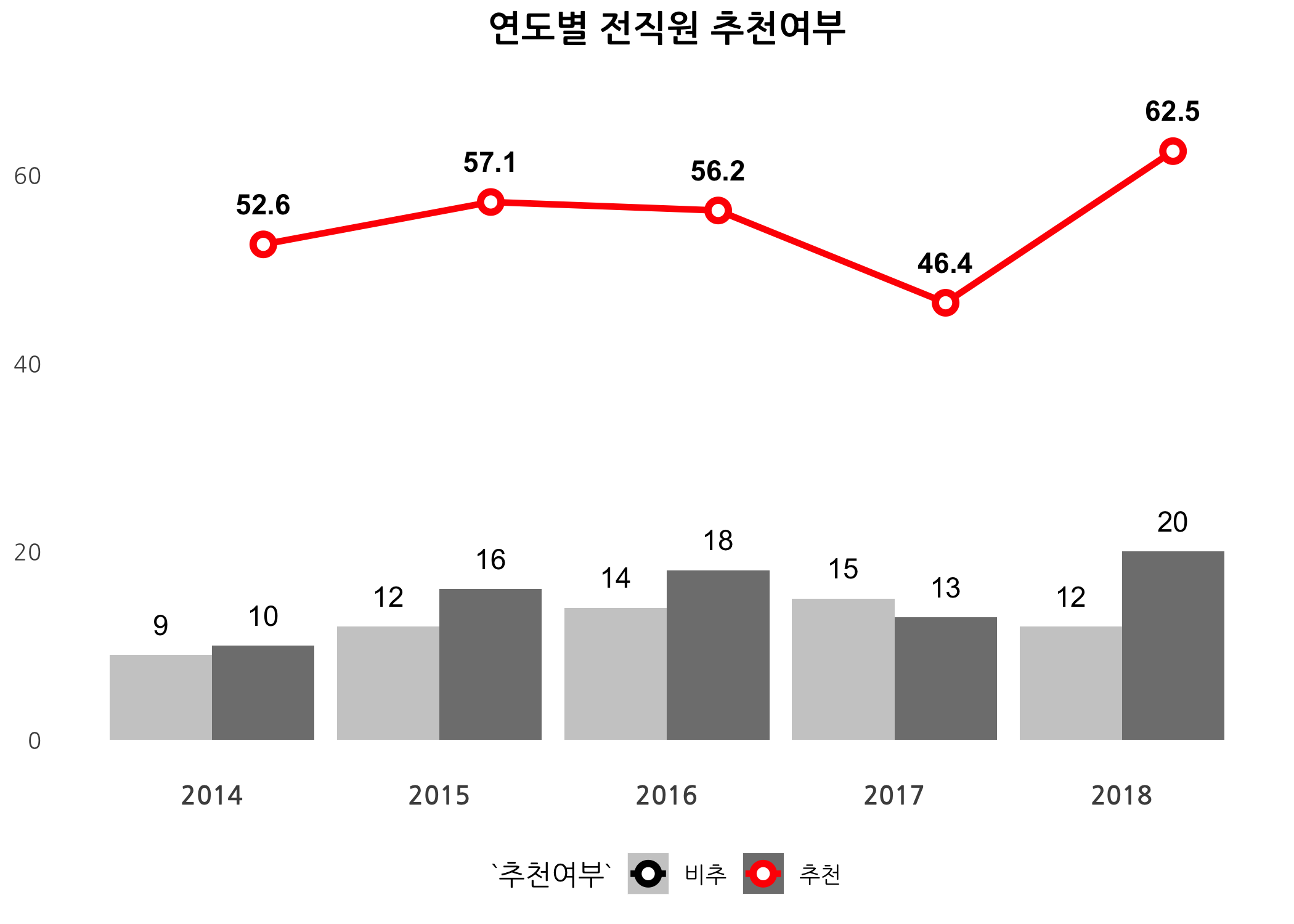
drawBarLinePlot(data = dt, workGb = '현직원', var = '성장예상')
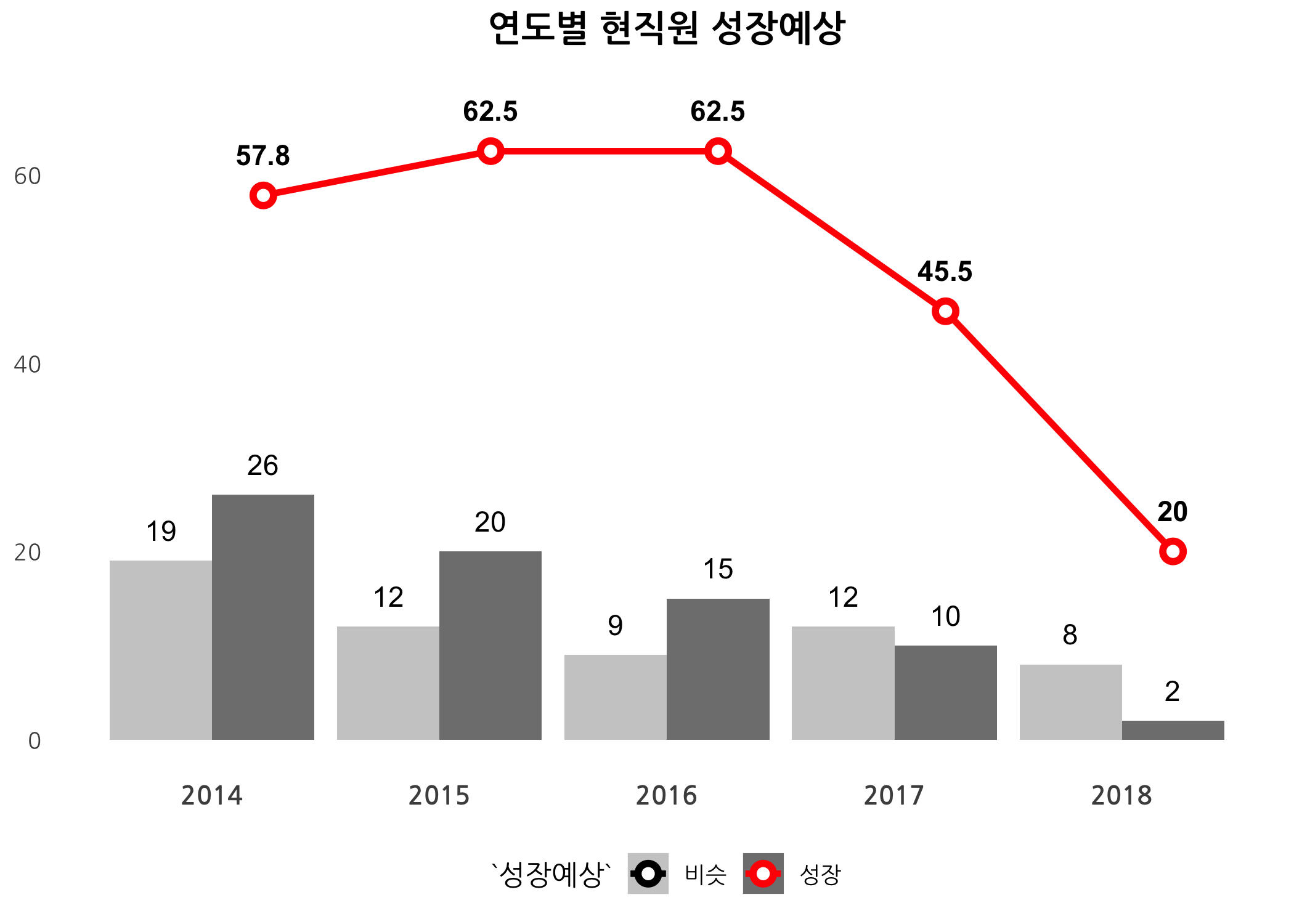
drawBarLinePlot(data = dt, workGb = '현직원', var = '추천여부')
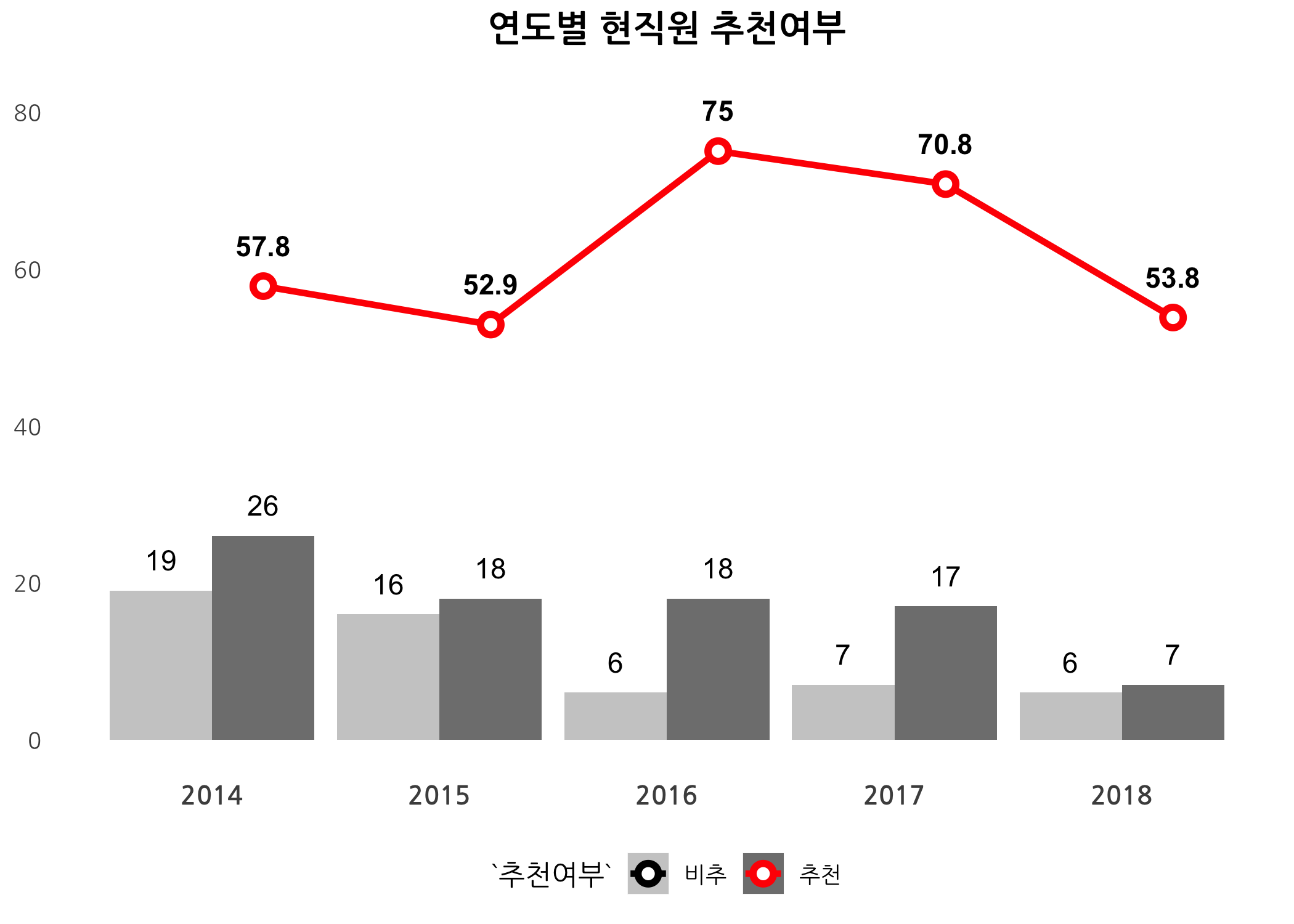
잡플래닛이 2014년부터 서비스를 시작했는데, 2016년을 기점으로 기업리뷰 등록되는 건수가 점차 감소하는 것으로 보입니다. 전직원의 성장예상은 점차 감소하는 추세를 보였고, 추천여부도 감소하는 듯 했으나 2018년도에 크게 반등하는 모습입니다. 혹시 2017년도에 인사팀에서 기업리뷰 관리를 안한 건 아닐지 모르겠네요.
현직원의 경우, 성장예상은 매년 큰 폭으로 감소하는데 특히 2018년에는 20%로 곤두박질쳤습니다. 추천여부도 크게 감소하였구요. 한 가지 특이한 점은, 2018년도 기업리뷰 신규 등록 건수입니다. 전직원은 32개였는데, 현직원은 13개입니다. 성장예상 컬럼은 NA가 많았는데 추천여부는 NA가 전혀 없었습니다. 2018년 이전에 회사를 떠난 사람들은 삼성화재를 아름답게 기억하고 있는지도 모르겠습니다. 아무튼 현직원들의 참여는 크게 감소했고, 참여한 사람들은 비관적은 견해를 올렸습니다.
재직상태별 별점 비중
잡플래닛 회원들은 기업리뷰를 남길 때 해당 회사에 대한 별점 평가를 1~5점으로 부여합니다. 1점이 가장 낮은 점수고 5점이 가장 높은 점수 입니다. 전체 총점과 다섯 가지 세부 항목 등 총 6가지 별점을 부여하는데요. 아래 그래프는 전체 총점에 대한 비중을 재직상태별로 비교한 것입니다.
# 재직상태에 따른 별점평가(총점) 빈도수를 확인합니다.
pts <- table(dt$재직상태, dt$별점평가) %>%
set_colnames(value = str_c('별점', 1:5)) %>%
as.data.frame() %>%
set_colnames(value = c('재직상태', '별점구분', '빈도수'))
# 필요한 패키지를 불러옵니다.
library(RColorBrewer)
library(JLutils)
# 나만의 팔레트를 생성합니다.
mypal <- brewer.pal(n = 9, name = 'Greys')
# 그래프를 그립니다.
ggplot(data = pts) +
aes(x = 재직상태, fill = 별점구분, weight = 빈도수) +
geom_bar(position = 'fill', color = 'gray80') +
geom_text(stat = 'fill_labels') +
scale_fill_manual(values = mypal[3:7]) +
ggtitle(label = '삼성화재 전/현직원 별점평가 비중') +
mytheme +
theme(axis.title = element_blank(),
axis.text.x = element_text(family = 'NanumGothic'),
axis.text.y = element_blank())
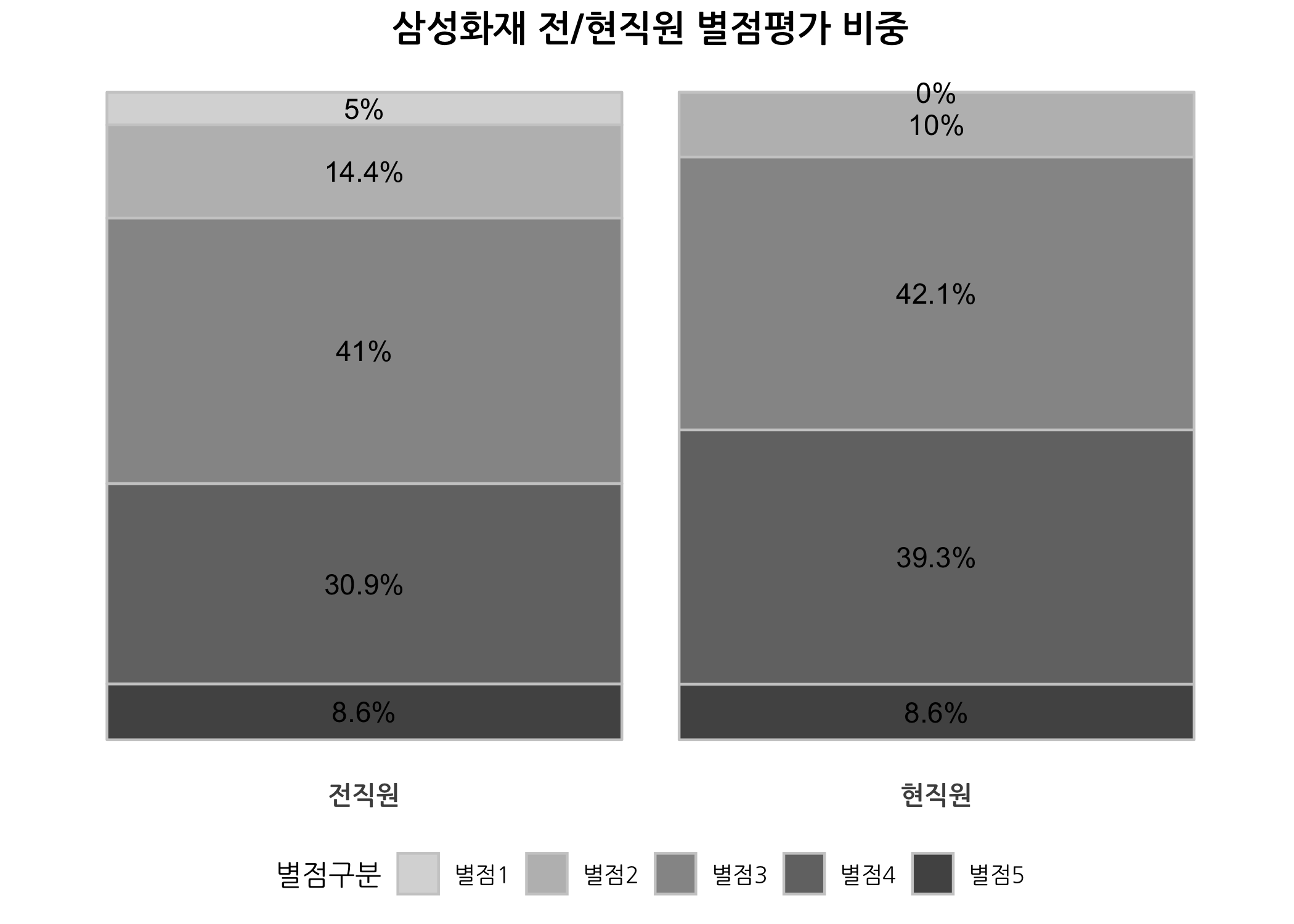
전직원과 현직원 간 차이가 많지 않습니다. 이 회사를 거쳐간 전직원의 80%는 별점이 3점 이상이라 생각하고 있고, 현직원은 90%가 3점 이상을 부여했습니다. 생각보다 평가를 잘받았네요.
레이더 차트 그리기
이번에는 6개 별점 항목 데이터를 이용하여 레이더 차트를 그려보겠습니다. 레이더 차트는 한 눈에 여러 가지 항목을 비교할 수 있다는 점에서 자주 사용됩니다.
# 필요한 패키지를 불러옵니다.
library(fmsb)
# 평균 별점 데이터 프레임을 생성합니다.
dt4radar1 <- dt %>%
dplyr::summarize(
전체평가 = mean(별점평가),
승진기회 = mean(승진기회),
복지급여 = mean(복지급여),
워라밸 = mean(워라밸),
사내문화 = mean(사내문화),
경영진 = mean(경영진)) %>%
as.data.frame()
# 결과를 출력합니다.
print(x = dt4radar1)
## 전체평가 승진기회 복지급여 워라밸 사내문화 경영진
## 1 3.351254 3.236559 4.114695 2.448029 3.086022 2.942652
# 그래픽 파라미터를 설정합니다.
par(mfrow = c(1, 1), mar = c(2, 1, 2, 1), family = 'NanumGothic')
# 레이더 차트를 그립니다.
radarchart(df = rbind(5, 1, dt4radar1),
axistype = 1,
seg = 4,
pty = 19,
pcol = rgb(red = 51/255, green = 0/255, blue = 255/255, alpha = 1.0),
plty = 1,
plwd = 2,
#pdensity = 10,
#pangle = 60,
pfcol = rgb(red = 51/255, green = 0/255, blue = 255/255, alpha = 0.2),
cglty = 1,
cglwd = 2,
cglcol = 'grey80',
axislabcol = 'grey30',
title = str_c(compNm, '의 평균 별점'),
vlcex = 1.2,
caxislabels = seq(from = 1, to = 5, by = 1) )
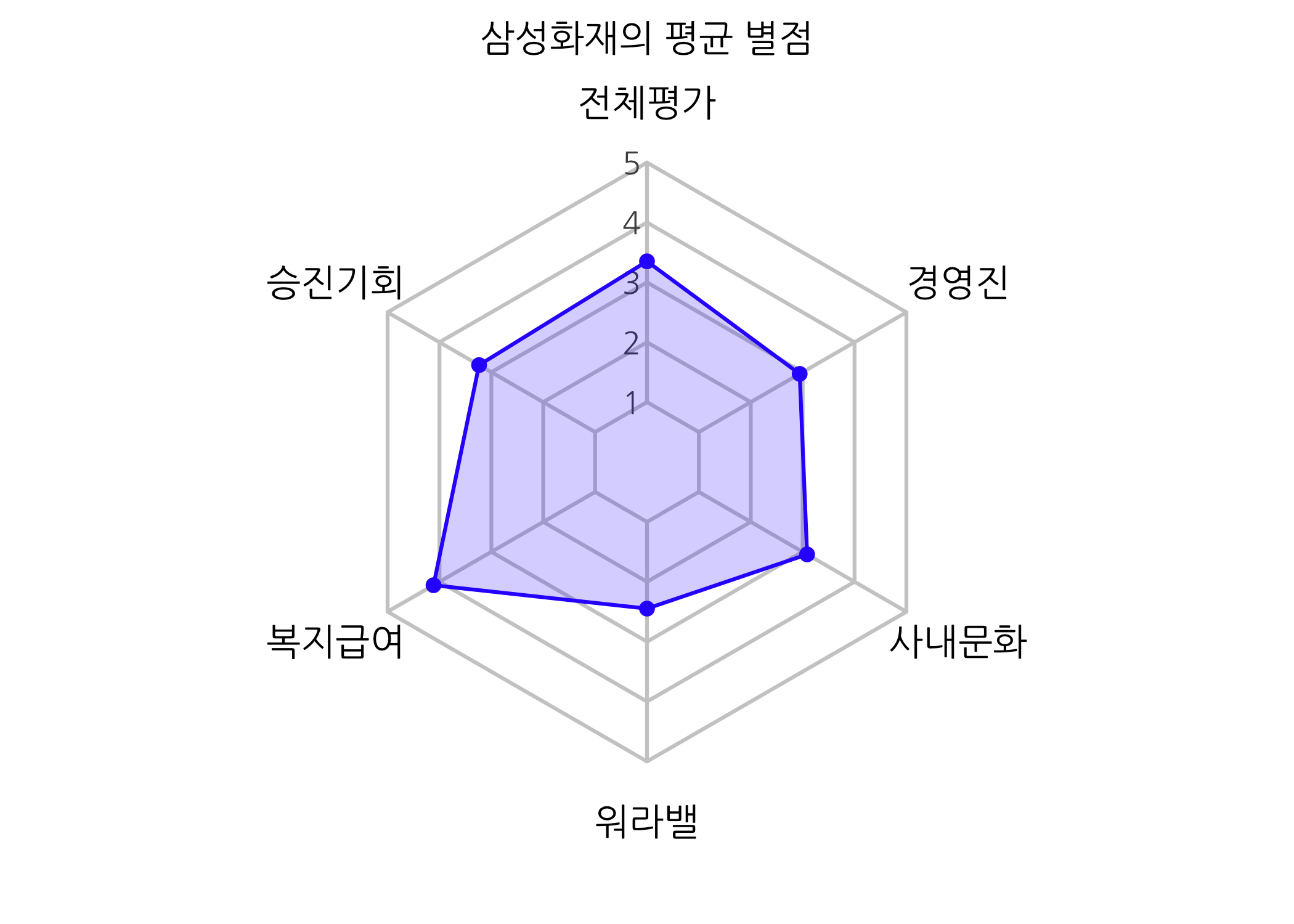
복지급여에서 가장 높은 점수를 받았고, 워라밸에서 가장 낮은 점수를 받았습니다. 여러분, 삼성이 이런 곳입니다. 개인 시간이 중요하지 않지만 높은 연봉이 중요한 사람들은 이 회사에 적극적으로 지원해보시면 될 것입니다.
그런데 재직상태별로는 어떻게 다를까요?
# 전/현직원의 평균 별점을 비교합니다.
dt4radar2 <- dt %>%
group_by(재직상태) %>%
dplyr::summarize(
전체평가 = mean(별점평가),
승진기회 = mean(승진기회),
복지급여 = mean(복지급여),
워라밸 = mean(워라밸),
사내문화 = mean(사내문화),
경영진 = mean(경영진)) %>%
as.data.frame()
# 별점 평균을 확인합니다.
print(x = dt4radar2)
## 재직상태 전체평가 승진기회 복지급여 워라밸 사내문화 경영진
## 1 전직원 3.237410 3.064748 4.028777 2.323741 2.985612 2.848921
## 2 현직원 3.464286 3.407143 4.200000 2.571429 3.185714 3.035714
# 재직상태별 테두리와 채우기 색을 설정합니다.
colorLines <- c(rgb(red = 255/255, green = 0/255, blue = 0/255, alpha = 1.0),
rgb(red = 51/255, green = 0/255, blue = 255/255, alpha = 1.0))
colorFills <- c(rgb(red = 255/255, green = 0/255, blue = 0/255, alpha = 0.2),
rgb(red = 51/255, green = 0/255, blue = 255/255, alpha = 0.2))
# 재직상태별 레이터 그래프를 하나의 하나의 그래프로 그립니다.
radarchart(df = rbind(5, 1, dt4radar2[, 2:7]),
axistype = 1,
seg = 4,
pty = 19,
pcol = colorLines,
plty = 1,
plwd = 2,
#pdensity = 10,
#pangle = 60,
pfcol = colorFills,
cglty = 1,
cglwd = 2,
cglcol = 'grey80',
axislabcol = 'grey30',
title = '재직상태별 평균 별점 비교',
vlcex = 1.2,
caxislabels = seq(from = 1, to = 5, by = 1) )
# 범주를 추가합니다.
legend(x = 0.8,
y = 1.4,
legend = dt4radar2$재직상태,
bty = 'n',
pch = 20,
col = colorLines,
text.col = 'grey30',
cex = 1,
pt.cex = 2)
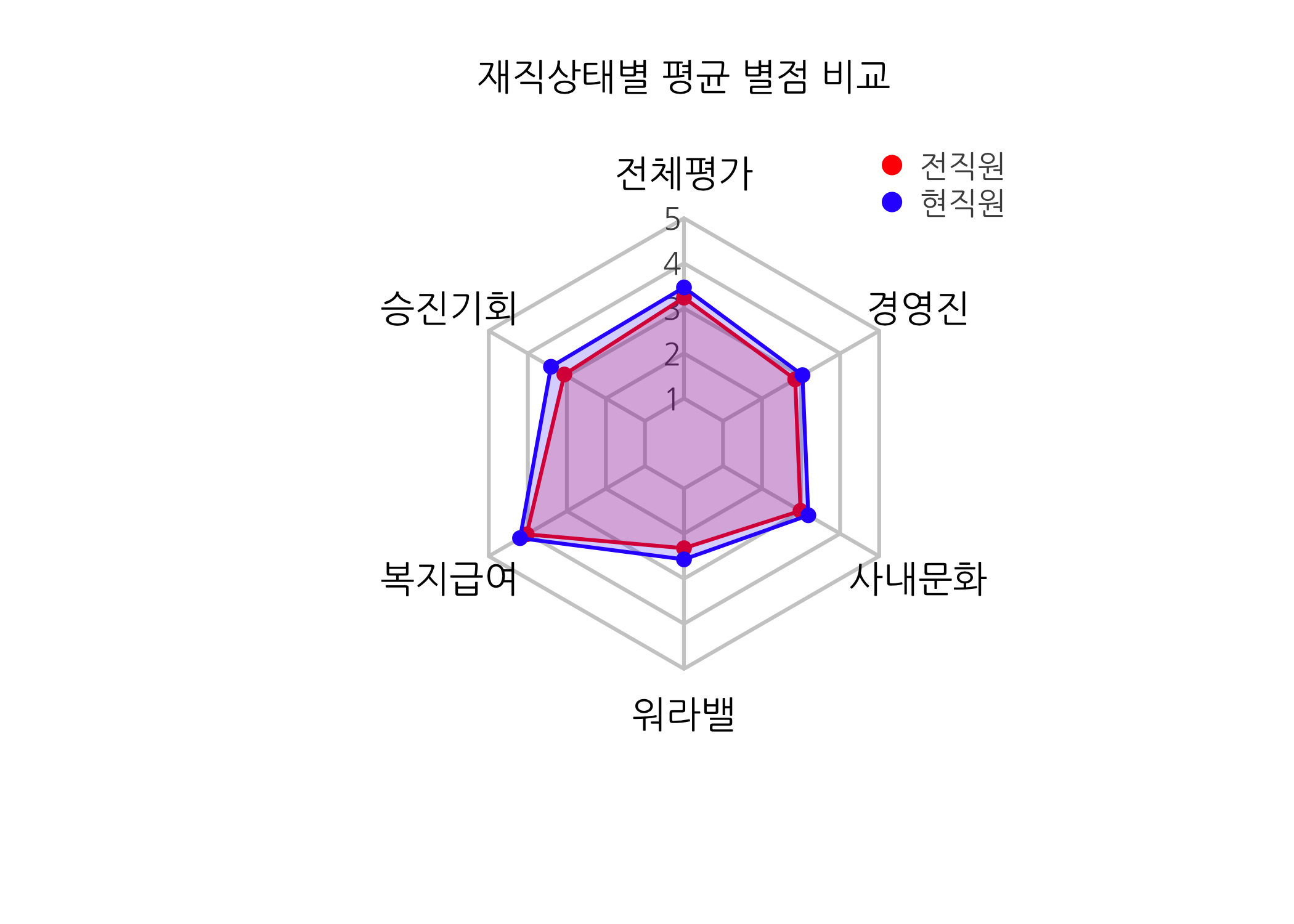
전직원은 빨간색, 현직원은 파란색(더 정확하게는 삼성블루)으로 표시해봤습니다. 전체 항목에서 현직원이 전직원보다 후한 평점을 부여한 것으로 보입니다. 다만 항목별로 차이가 나는 부분이 보이는데요. 승진기회와 워라밸에서 차이가 컸습니다. 반대로 복지급여는 가장 차이가 작네요. 복지제도와 연봉 수준이 정말 높은가 봅니다. 제 기억으로도 돈을 많이 받았던 것 같습니다.
탐색적 데이터 분석은 이 정도로 마치고 추천에 영향을 주는 변수들은 무엇인지 분류모형을 적합해보도록 하겠습니다.
의사결정나무를 활용한 추천모형
의사결정나무는 분류모형을 만드는 데 많이 사용되는 알고리즘입니다. 현업 분석가들이 가장 애용하는 알고리즘 중 하나죠. 만들기 쉽고 활용하기 쉽기 때문입니다.
분석 모델링을 하기에 앞서 전체 데이터를 70%대 30%으로 샘플링해서 각각 훈련셋(training set)과 시험셋(test set)으로 분할하도록 하겠습니다. 사실 이 정도로 데이터의 규모가 작을 때는 교차 검증(Cross validation)을 하는 편이 낫습니다만, 이번 포스팅에서는 편의상 자료분할 검증(Hold-out validation) 방법을 사용하겠습니다. 별도로 검증셋(validation set)은 만들지 않았습니다.
# 필요한 컬럼만 선택하여 데이터셋을 생성합니다.
dt <- dt %>% select(c('승진기회', '복지급여', '워라밸', '사내문화', '경영진', '추천여부'))
# 재현 가능하도록 시드를 생성합니다.
set.seed(seed = 123)
# 전체 데이터를 임의로 샘플링하기 위해 다음과 같이 처리합니다.
# 훈련셋을 70%, 시험셋을 30%로 할당합니다.
idx <- sample(x = 2, size = nrow(x = dt), prob = c(0.7, 0.3), replace = TRUE)
# idx가 1일 때 훈련셋(trset), 2일 때 시험셋(teset)에 할당됩니다.
trset <- dt[idx == 1, ]
teset <- dt[idx == 2, ]
cat('The number of trset is', nrow(x = trset), '!\n')
## The number of trset is 201 !
cat('The number of teset is', nrow(x = teset), '!\n')
## The number of teset is 78 !
# 훈련용, 시험용 데이터셋의 목표변수 비중을 확인합니다.
rbind(dt$추천여부 %>% table() %>% prop.table() %>% t(),
trset$추천여부 %>% table() %>% prop.table() %>% t(),
teset$추천여부 %>% table() %>% prop.table() %>% t()) %>%
`*`(100) %>%
round(digits = 2L) %>%
set_rownames(c('전체', '훈련셋', '시험셋')) %>%
print()
## 비추 추천
## 전체 41.58 58.42
## 훈련셋 41.29 58.71
## 시험셋 42.31 57.69
목표변수를 추천여부로 설정하고, 전체 데이터와 훈련셋 및 시험셋의 빈도를 확인해보니 치우침없이 샘플링이 된 것 같습니다. 이제 이 데이터셋으로 모형을 적합하고 분류 성능을 확인하겠습니다.
가지치기 전 나무모형
의사결정나무는 이상치에 영향을 받지 않고 비모수적 알고리즘이라 쉽게 만들 수 있다는 장점이 있지만 과적합되기 쉽다는 단점이 있습니다. 따라서 초기 모형을 적합한 다음 비용복잡도 기준으로 가지치기를 실시해야 합니다. 일단 초기 모형을 적합하기 위해 순수도 계산 기준으로 gini index를 사용하였습니다.
# 필요한 패키지를 불러옵니다.
library(rpart)
library(rpart.plot)
library(caret)
# 의사결정나무 알고리즘을 이용하여 추천 분류모형을 적합합니다.
fit <- rpart(formula = 추천여부 ~ .,
data = trset,
method = 'class',
parms = list(split = 'gini'),
control = rpart.control(
minsplit = 20,
cp = 0.01,
maxdepth = 10))
# 그래픽 파라미터를 설정합니다.
par(mfrow = c(1, 1), mar = c(5, 4, 4, 2), family = 'NanumGothic')
# 나무모형을 출력합니다.
print(x = fit)
## n= 201
##
## node), split, n, loss, yval, (yprob)
## * denotes terminal node
##
## 1) root 201 83 추천 (0.41293532 0.58706468)
## 2) 사내문화< 2.5 56 15 비추 (0.73214286 0.26785714)
## 4) 경영진< 1.5 15 0 비추 (1.00000000 0.00000000) *
## 5) 경영진>=1.5 41 15 비추 (0.63414634 0.36585366)
## 10) 승진기회< 3.5 33 10 비추 (0.69696970 0.30303030) *
## 11) 승진기회>=3.5 8 3 추천 (0.37500000 0.62500000) *
## 3) 사내문화>=2.5 145 42 추천 (0.28965517 0.71034483)
## 6) 경영진< 3.5 93 36 추천 (0.38709677 0.61290323)
## 12) 워라밸< 1.5 20 8 비추 (0.60000000 0.40000000) *
## 13) 워라밸>=1.5 73 24 추천 (0.32876712 0.67123288)
## 26) 승진기회< 3.5 51 22 추천 (0.43137255 0.56862745)
## 52) 승진기회< 2.5 13 5 비추 (0.61538462 0.38461538) *
## 53) 승진기회>=2.5 38 14 추천 (0.36842105 0.63157895)
## 106) 경영진< 2.5 9 4 비추 (0.55555556 0.44444444) *
## 107) 경영진>=2.5 29 9 추천 (0.31034483 0.68965517) *
## 27) 승진기회>=3.5 22 2 추천 (0.09090909 0.90909091) *
## 7) 경영진>=3.5 52 6 추천 (0.11538462 0.88461538) *
rpart.plot(x = fit, main = '가지치기 전 추천모형')
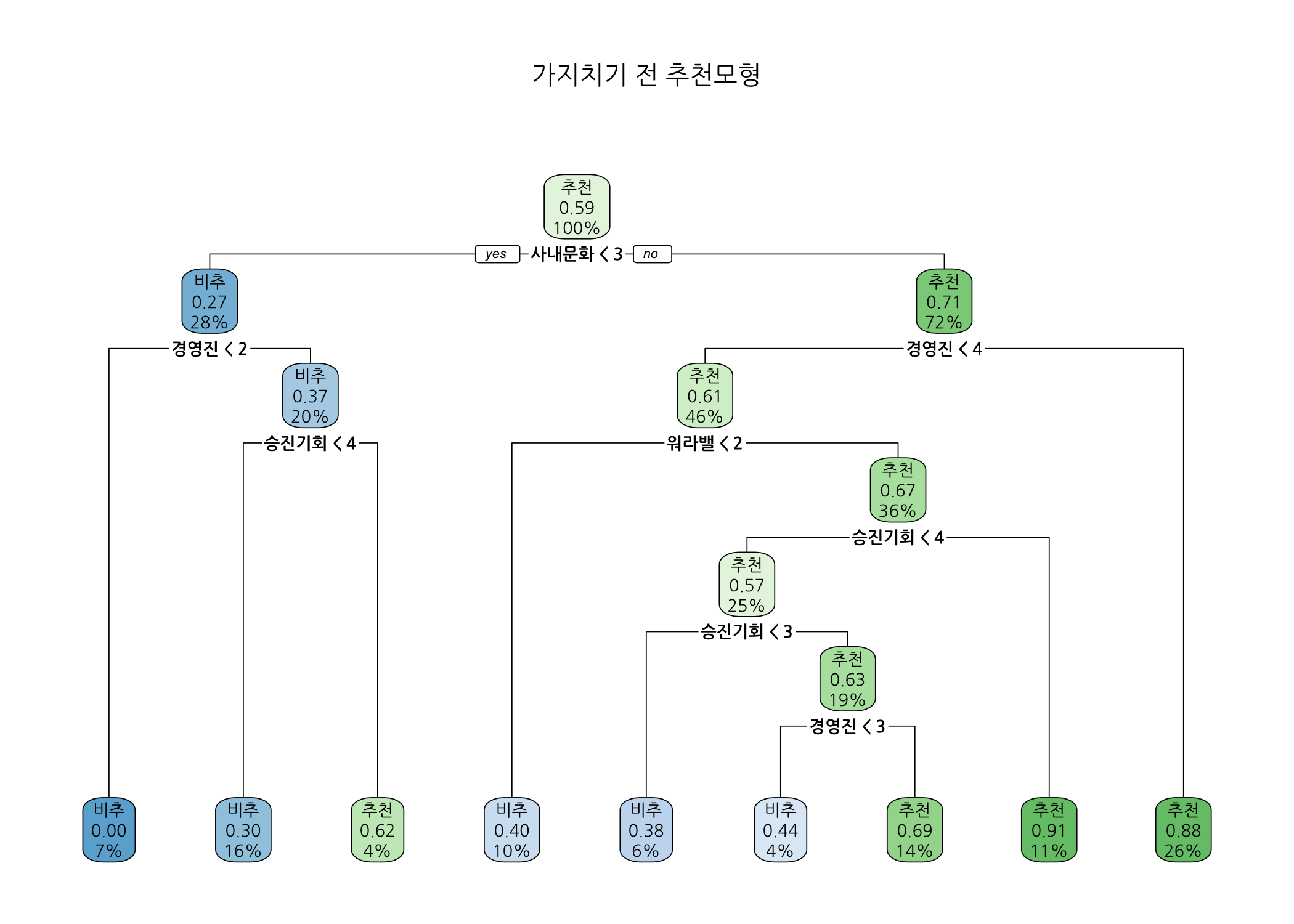
나무모형 그래프를 살펴보니, 가장 최상위 노드를 보면 추천 비중이 59%이고 전체 훈련셋의 100%가 이 노드에 속해 있습니다. 끝 노드가 모두 9개였는데 추천 비중이 0%에서 91%까지 다양했습니다. 가장 처음 분리에 사용된 입력변수는 사내문화로 1~2점을 부여한 회원의 27%만 추천한 반면, 3점 이상 부여한 회원은 71%가 추천하였습니다. 다음으로 사용된 입력변수는 경영진으로 1점을 부여한 회원은 삼성화재를 추천하지 않았습니다. 아마도 경영진에 대한 실망이 상당히 컸나 봅니다. 계속해서, 경영진에 대한 평가가 2점 이상인 회원 중 승진기회가 3점 이하인 경우 30%가 추천한 반면 4점 이상인 경우 평균보다 높은 62%가 추천하였습니다. 승진기회가 높다고 판단한 회원은 삼성화재에서 잘나가는 임직원인가 봅니다.
사내문화에 대한 별점이 3점 이상이고 경영진에 대한 별점이 4점 이상인 경우, 88%가 삼성화재를 추천했습니다. 이 회사가 군대문화로 유명한데 이 그룹에 속하는 회원들은 좀 독특한 것 같습니다. 실제로 의사결정나무 알고리즘을 이용하여 고객 세분화에도 사용하니까 비슷한 성향을 갖는 회원들이 모여있다고 봐도 무방하겠습니다.
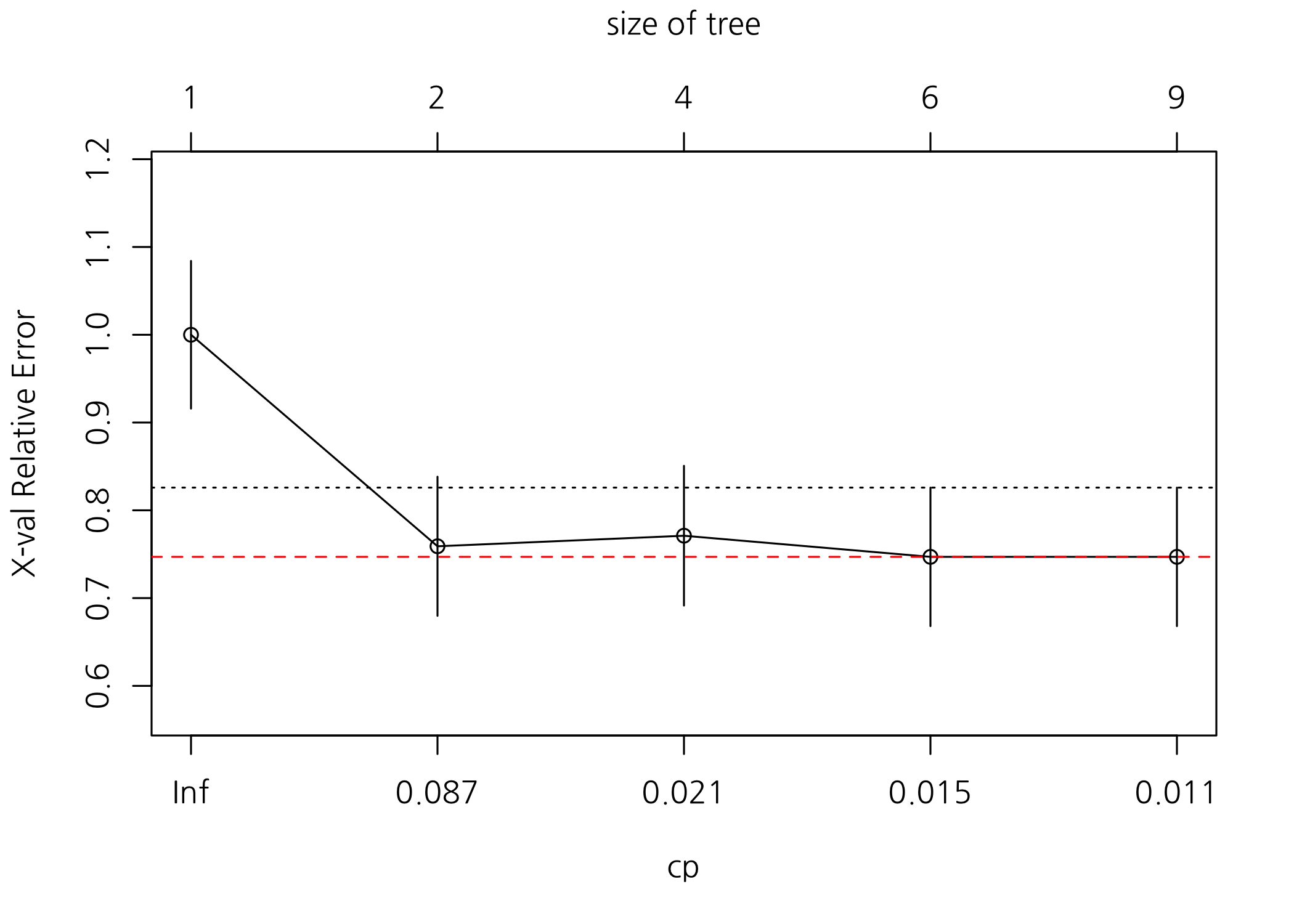
이제 가지치기를 해보겠습니다. 가지치기는 비용복잡도(Cost complexity)를 기준으로 xerror가 가장 낮을 때의 파라미터(cp)를 이용합니다.
# 비용복잡도(Cost Complexity) 표를 출력합니다.
printcp(x = fit)
##
## Classification tree:
## rpart(formula = 추천여부 ~ ., data = trset, method = "class",
## parms = list(split = "gini"), control = rpart.control(minsplit = 20,
## cp = 0.01, maxdepth = 10))
##
## Variables actually used in tree construction:
## [1] 경영진 사내문화 승진기회 워라밸
##
## Root node error: 83/201 = 0.41294
##
## n= 201
##
## CP nsplit rel error xerror xstd
## 1 0.313253 0 1.00000 1.00000 0.084102
## 2 0.024096 1 0.68675 0.75904 0.079238
## 3 0.018072 3 0.63855 0.77108 0.079575
## 4 0.012048 5 0.60241 0.74699 0.078891
## 5 0.010000 8 0.56627 0.74699 0.078891
# 교차확인 상대오차 도표를 확인합니다.
plotcp(x = fit)
abline(h = fit$cptable[, 'xerror'] %>% min(), col = 'red', lty = 2)
# xerror이 가장 낮을 때의 비용복잡도 파라미터를 구합니다.
bestCP <- fit$cptable[which.min(fit$cptable[ , 'xerror']), 'CP']
# 가지치기(pruning)를 합니다.
prn <- prune.rpart(tree = fit, cp = bestCP)
# 가지치기 후 나무모양을 출력합니다.
print(x = prn)
## n= 201
##
## node), split, n, loss, yval, (yprob)
## * denotes terminal node
##
## 1) root 201 83 추천 (0.41293532 0.58706468)
## 2) 사내문화< 2.5 56 15 비추 (0.73214286 0.26785714) *
## 3) 사내문화>=2.5 145 42 추천 (0.28965517 0.71034483)
## 6) 경영진< 3.5 93 36 추천 (0.38709677 0.61290323)
## 12) 워라밸< 1.5 20 8 비추 (0.60000000 0.40000000) *
## 13) 워라밸>=1.5 73 24 추천 (0.32876712 0.67123288)
## 26) 승진기회< 3.5 51 22 추천 (0.43137255 0.56862745)
## 52) 승진기회< 2.5 13 5 비추 (0.61538462 0.38461538) *
## 53) 승진기회>=2.5 38 14 추천 (0.36842105 0.63157895) *
## 27) 승진기회>=3.5 22 2 추천 (0.09090909 0.90909091) *
## 7) 경영진>=3.5 52 6 추천 (0.11538462 0.88461538) *
rpart.plot(x = prn, main = '가지치기 후 추천모형')
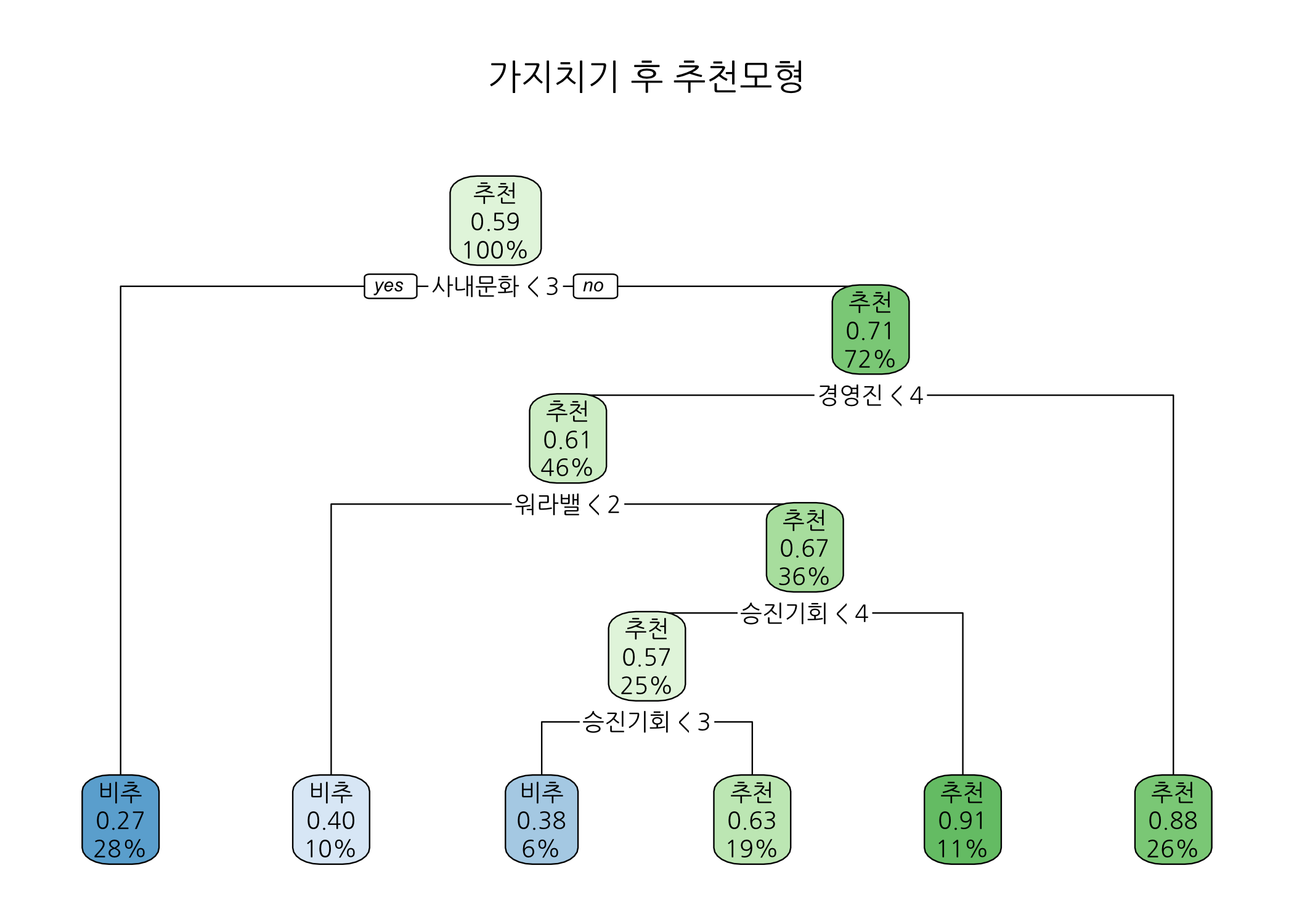
가지치기를 하고 나니 끝 노드의 수가 6개로 줄었습니다. 가지치기를 하고 나면 나무모형이 간결해지고 과적합 위험이 감소하는 효과가 있습니다. 가지치기 후 추천모형을 살펴보면, 사내문화가 가장 먼저 사용되었고 다음으로 경영진과 워라밸이 뒤를 이었습니다. 이는 무엇을 의미할까요? 제 생각에는 회사마다 고유한 기업문화를 가지고 있는데, 그 기업문화에 적응하는 사람과 그렇지 못한 사람들의 평가가 가장 극명하게 갈린다고 판단됩니다. 대기업에 다니는 임직원 입장에서는, 회사의 조직문화에 익숙해지려고 노력해야 할 것입니다. 회사 입장에서는 슈퍼 갑 행세를 할 수 있을테니 임직원 개개인이 조직문화에 적응을 하든지 말든지 크게 개의치 않을 것 같구요. 물론 개인의 역량이 아주 뛰어난 임직원이라면 어떨까요? 그래도 별로 상관 안할 것 같아요. 워낙에 큰 회사라 말이죠.
분류모형의 성능 평가
마지막으로 분류모형의 성능을 평가하는 과정을 진행해보겠습니다. 방금 우리가 만든 추천모형에 시험셋을 할당하여 추정값을 계산해냅니다. 그리고 시험셋의 실제값과 추정값으로 분류모형의 성능을 평가할 수 있는데요. 크게 3가지 방법이 사용됩니다.
혼동행렬(Confusion Matrix)을 이용한 성능 평가
# 실제값을 지정합니다.
real <- teset$추천여부
# 시험셋으로 추정값을 생성합니다.
pred <- predict(object = prn, newdata = teset, type = 'class')
# 혼동행렬을 사용하여 모형의 분류 성능을 파악합니다.
confusionMatrix(data = pred, reference = real, positive = '추천')
## Confusion Matrix and Statistics
##
## Reference
## Prediction 비추 추천
## 비추 18 8
## 추천 15 37
##
## Accuracy : 0.7051
## 95% CI : (0.5911, 0.803)
## No Information Rate : 0.5769
## P-Value [Acc > NIR] : 0.01356
##
## Kappa : 0.3784
## Mcnemar's Test P-Value : 0.21090
##
## Sensitivity : 0.8222
## Specificity : 0.5455
## Pos Pred Value : 0.7115
## Neg Pred Value : 0.6923
## Prevalence : 0.5769
## Detection Rate : 0.4744
## Detection Prevalence : 0.6667
## Balanced Accuracy : 0.6838
##
## 'Positive' Class : 추천
##
혼동행렬의 결과로 여러 숫자가 어지럽게 출력되었습니다만, 우리가 주목해야 할 점은 민감도(Sensitivity)와 특이도(Specificity), 그리고 정밀도(Pos Pred Value)입니다. 민감도는 실제값이 Postive인 것 중 추정값이 Positive인 비율이고, 반대로 특이도는 실제값이 Negative인 것 중 추정값이 Negative인 비율입니다. 정밀도는 추정값이 Positive인 것 중 실제값이 Positive인 것인데요. 혼동행렬에 대해서 궁금하신 분은 따로 공부를 하셔야 할 것입니다.
여기에서 다룰 내용은 이 세 가지 값이 클수록 좋다는 것입니다. 만약 여러 알고리즘을 사용하고, 변수 선택을 다르게 하여 다수의 모형을 만들었을 때 세 가지 값을 비교해야 하는데요. 그럴 때 어떤 기준으로 하면 좋을지 혼동이 될 수가 있습니다. (그래서 혼동행렬인가요???)
이런 경우, F1 점수나 AUROC값을 활용하면 됩니다. 둘 다 0에서 1 사이의 값을 갖습니다.
F1 점수는 민감도와 정밀도의 조화평균 값입니다. 두 가지 모두 커야 이 값이 커집니다. 조화평균은 속도의 평균을 생각하시면 됩니다.
# 필요한 패키지를 불러옵니다.
library(MLmetrics)
# F1 score를 확인합니다.
cat('F1 score :', F1_Score(y_true = real, y_pred = pred, positive = '추천'), '\n')
## F1 score : 0.7628866
F1 점수가 0.7628866이면 분류 성능이 우수하다고 할 수 없습니다. 데이터의 한계라고 생각됩니다.
다음으로 AUROC를 확인해보겠습니다. AUROC는 ROC 커브의 아래 면적을 의미합니다. ROC 커브는 민감도와 1-특이도를 양 축으로 하여 그린 그래프입니다. 두 가지 값이 클수록 왼쪽 상단 모서리에 가까운 그래프가 그려지고, AUROC가 1에 가까운 값을 가지게 됩니다. 그림으로 확인하시죠.
# ROC curve와 AUROC에 필요한 패키지를 불러옵니다.
library(ROCR)
library(pROC)
# ROC 커브를 그려서 분류 성능을 확인합니다.
# 추정값 및 실제값이 범주형인 경우, 숫자 벡터로 변환합니다.
predObj <- prediction(predictions = pred %>% as.numeric(),
labels = real %>% as.numeric())
# prediction 객체를 활용하여 performance 객체를 생성합니다.
perform <- performance(prediction.obj = predObj, measure = 'tpr', x.measure = 'fpr')
# ROC 커브를 그립니다.
plot(x = perform, main = str_c('[ROC & AUROC] ', compNm))
# 왼쪽 아래 모서리에서 오른쪽 위 모서리를 잇는 대각선을 추가합니다.
lines(x = c(0, 1), y = c(0, 1), col = 'red', lty = 2)
# AUROC를 계산하고 ROC 커브 위에 출력합니다.
auroc <- auc(response = real %>% as.numeric(),
predictor = pred %>% as.numeric()) %>%
round(digits = 4L)
text(x = 0.9, y = 0, labels = str_c('AUROC : ', auroc), col = 'red')
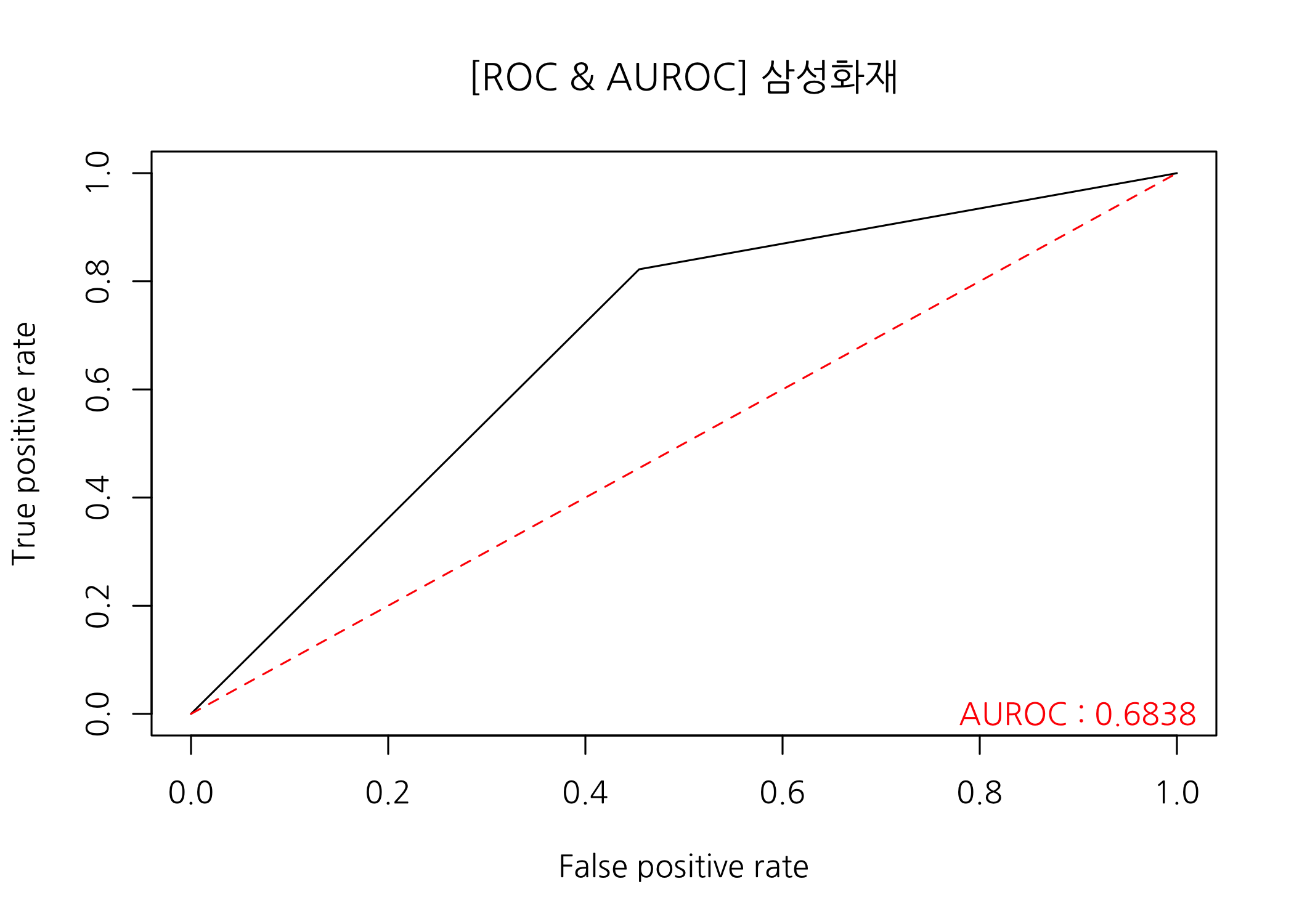
print(x = auroc)
## [1] 0.6838
ROC 커브의 모양도 그렇고 AUROC 값도 0.6838로 크게 낮습니다. 다른 변수를 추가할 수 있으면 좋을 것 같습니다. 예를 들어, 인사팀 직원 여부라든가 실제로 근무했는지 여부를 알 수 있다면 어떤 결과가 나올지 궁금합니다.
혹시 재직상태별로 모형을 나누어 적합해보면 어떨까요? 사실 우리는 맨 처음에 카이제곱 검정을 통해 재직상태와 추천여부에 영향을 주지 않는다는 것을 확인했습니다. 그래도 학습을 위해 한 번 해보시는 건 어떨까요?
이번 포스팅은 이걸로 마무리하겠습니다. 읽어주셔서 감사합니다!